如何评价临床试验中盲法实施是否成功？

　　盲法（blinding）在临床试验中的历史可以追溯到两三个世纪前。它在流行病学研究中的应用是伴随着安慰剂效应的发现而开始的。1799年，当时流行一种叫做“Perkins tractors”的金属棒，据宣称它可以把身体中的疾病“抽出”从而治疗疾病，而且售价昂贵。John Haygarth医生认为这样的售价并无意义，所以用一套木制的“Perkins tractors”作为安慰剂与金属棒比较效果，发现木棒也具有类似金属棒的“治疗效果”（即安慰剂效应），从而打破了人们的误解，因为他们认为之前的疗效是由这种金属棒的磁场所产生的。[1]这个试验被认为是流行病学中单盲试验的先驱之一，但是这个试验只做到了单盲，即受试者盲。医生或疗效评价者仍然知晓治疗的分配，所以后来还出现了双盲试验，即受试者和医生均不知晓分组情况，如1931年Amerson治疗肺结核的研究中以及1911年Bingel在治疗白喉的研究中均采用了双盲，即患者和参与医生均不知晓分组方式。

　　虽然几乎所有人都能够理解盲法的概念，但是事实上，很多研究者仍然把盲法和分配隐藏（allocation concealment）混淆。分配隐藏的目的是为了保证盲法的成功实施，它是实施盲法的必要条件但并非盲法本身，盲法的目的是指让受试者、研究者、疗效评价者无法分辨出是谁接受了何种治疗，实施盲法主要是出于以下两个目的：
　　A: 减少对结局事件的差异性评估
　　B: 提高受试者的依从性

　　对于目的A，想象一下如果结局事件是一种主观评价，如果疗效的评价者已经知道了对方所使用的是阳性药物，那么可能会影响他们对于结果的评估；对于目的B，如果受试者已经知道了自己使用的是安慰剂（placebo），那么他/她可能会很容易违背试验方案，或者寻求其他治疗措施，甚至直接拒绝继续参与该试验。

　　下表总结了在临床试验中对不同角色实施盲法的作用[2]

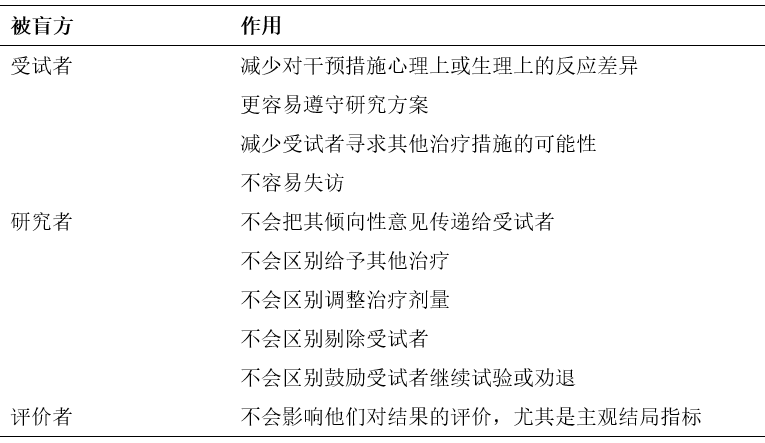
　　尽管很多研究者都会宣称自己做到了“双盲”，“三盲”甚至更多（比如把统计师盲也考虑在内），通常的说辞是“研究者、受试者、疗效评价者均被盲”，或者再加上一句“患者和医生都无法分辨阳性药物和安慰剂，它们的外观、形状、颜色、气味相同”。However, talk is cheap. 轻描淡写地在报告中描述这样一句话的分量实在难以让人信服。根据CONSORT指南的建议，研究者不仅仅需要报告是否进行了盲法的应用，同时还需要具体的盲法实施细节及步骤，以及盲法的实施是否成功。[3]

　　那么，临床试验中如果出现了阳性药物与安慰剂的对照，如何判断试验的参与者无法分辨出自己服用的是阳性药物还是安慰剂呢？或者说如何判断盲法的实施是否成功？

　　首先可能会想到的是可以采用卡方检验（chi-squared test）或者kappa一致性检验（kappa statistic）来计算阳性药物组和安慰剂组的人群对于自己所使用药物的选择是否存在一致性（比如药物组85%的人认为自己使用了药物，安慰剂组中80%的人也认为自己使用了药物而非安慰剂）。这样是很有道理的，但是对于专门的盲法评价却存在一些方法学上的缺陷，并且结果数据解释和实际情况可能存在误差，如果仅仅依赖于卡方检验的p值结果或kappa系数，可能即使最终取得了较高的p值或者较好的一致性解释，但实际上，两组均已破盲，即较好的一致性既可以说明盲法比较成功，也可能说明盲法比较失败。

　　基于存在的问题，1996年James等人在STATISTICS IN MEDICINE上发表了题为An index for assessing blindness in a multi-centre clinical trial: disulfiram for alcohol cessation--a VA cooperative study的研究论文，通过一项临床随机对照试验的应用实例系统介绍了James index的理论和应用。[4]其主要原理是基于kappa系数的变化，但是kappa系数仅能适用于因变量为二分类的情况（如是/否），但在临床试验中除了是/否的选择外，有时患者其实并无法判断自己接受的何种疗法，即需要第三个选项“不知道”来满足这一部分人群的选择。James index扩展了传统kappa系数的适用范围，增加了“不知道”这个选择的范围。

　　James Index的计算公式如下：

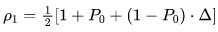
[公式] （1）

　　最终可得到一个[0, 1]范围的值，越高的值代表越成功的盲法，因此 [公式] = 1时代表完全成功的盲法，等于0时则代表盲法失败，等于0.5时则代表完全随机盲法（一半正确一半不正确）。其结果的95%置信区间的上界如果在0.5的左侧则说明盲法可能失败，或者说试验可能破盲。统计量[公式]代表相信自己所在组别的人群分布。

[公式] (2)

　　其中，

　　a表示组别；a = T代表治疗组，a = C代表安慰剂组；

　　g表示受试者的个人猜测，g = -代表相信自己在安慰剂组，g = +则代表相信自己在治疗组，g = 0则代表不确定自己的分组；

　　p_ag表示受试者分配组别及猜测的比例；

　　p_a表示受试者的组别分配比例 ；

　　p_g表示受试者的猜测比例；

　　omega_ag表示对于正确和错误猜测相对分布的加权

　　James index考虑到了“don't know”的情况，相对于传统的kappa统计量用以评价临床试验的盲法成功性更有意义，但是由于它合并了所有组别数据（药物组+对照组），所以无法分辨组间差异，因此可能也会造成对结果的曲解（如安慰剂组破盲，但因药物组盲法十分成功，造成了总体结果被稀释）。

　　后来，Bang等人进一步提出了Bang's index来评价盲法成功性。[5]和James index类似，通过Bang's index也可计算出一个包含方向的区间，但这个区间范围为[-1, 1]，其中正值代表盲法失败（即多数受试者猜中了分配组别），负值则代表盲法成功（即多数受试者猜错了分配组别），0则代表理想的盲法结果。

　　Bang's Index的计算公式如下：

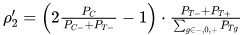
[公式] (3)

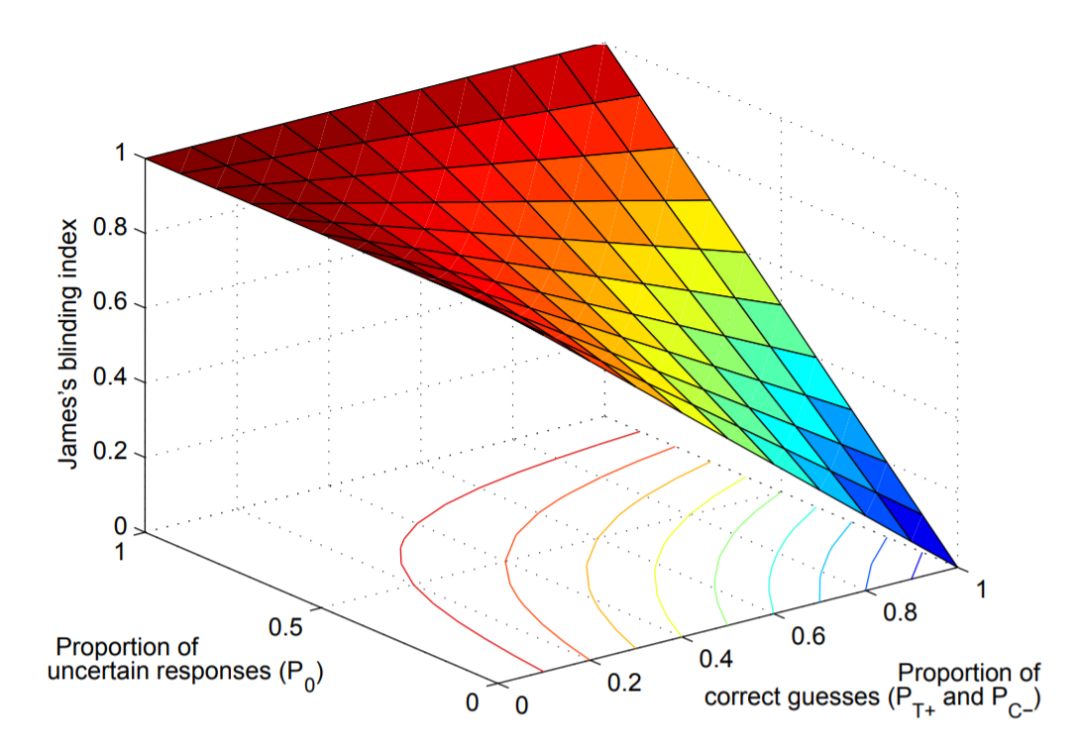
　　图a 受试者猜测正确和不确定的比例及与James index的关系 (Ognjen Arandjelovic, NIPS)

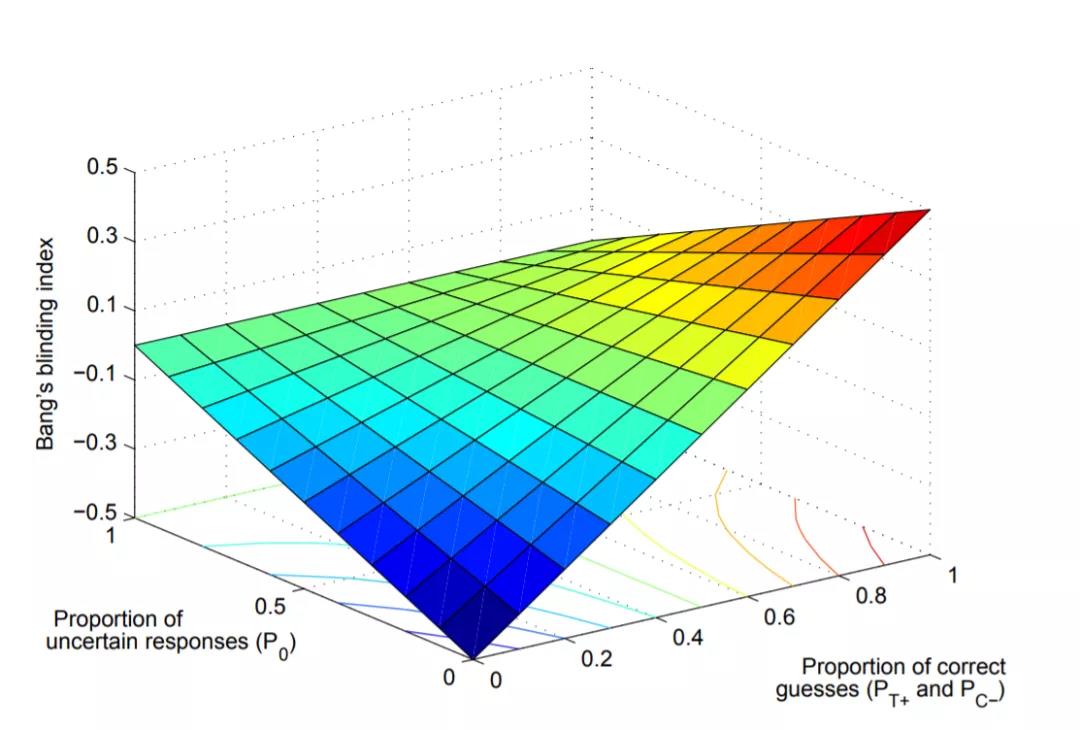
　　图b 受试者猜测正确和不确定的比例及与Bangs index的关系 (Ognjen Arandjelovic, NIPS)

　　由（1）可知James index过于依赖于P0也就是选择了“不清楚”的受试者，但实际上这一类人群并不是真的不清楚，这样做容易造成了信息偏倚和结果的错误解释。Bang's index则更多依赖于明确做出选择的受试者进行计算。

　　除了以上方法外还有一些可以评价盲法成功性的统计学方法，比如图片a/b来源的中的NIPS论文，[6]根据作者Ognjen Arandjelovic的说明，他们开发了一种新的方法弥补了之前两种index的不足，可以使得结果更加稳健不易受到影响。有兴趣的朋友可以自行了解。但需要强调的是，评价盲法成功与否固然重要，但更重要的是在研究设计阶段和实施阶段要尽可能的同时考虑目的、方法、风险、伦理等因素，保证盲法的成功在于多方考虑和平衡取舍，而再完美的post hoc检验对于一项已经失败的盲法也已经太晚了。

　　作者简介

　　秦宗实，香港大学李嘉诚医学院中药学专业在读博士，研究方向为天然药物与神经疾病的转化医学研究。曾参与“十二五”国家科技支撑计划项目、国家重点研发计划“中医药现代化研究”重点专项等临床研究，参与研究方案及统计分析计划制定。在J Urol、Am J Med、Mayo Clinic Proc、Brain Behav Immun等期刊发表论文20多篇。

　　参考文献

　　1 https://en.wikipedia.org/wiki/John_Haygarth
　　2 https://www.amazon.com/Handbook-Essential-Concepts-Clinical-Handbooks/dp/0080448666
　　3 http://www.consort-statement.org/
　　4 https://onlinelibrary.wiley.com/doi/abs/10.1002/%28SICI%291097-0258%2819960715%2915%3A13%3C1421%3A%3AAID-SIM266%3E3.0.CO%3B2-H
　　5 https://www.sciencedirect.com/science/article/abs/pii/S0197245603001776?via%3Dihub
　　6 https://papers.nips.cc/paper/4722-assessing-blinding-in-clinical-trials.pdf